FINAL SUMMARY

LINKED LIST

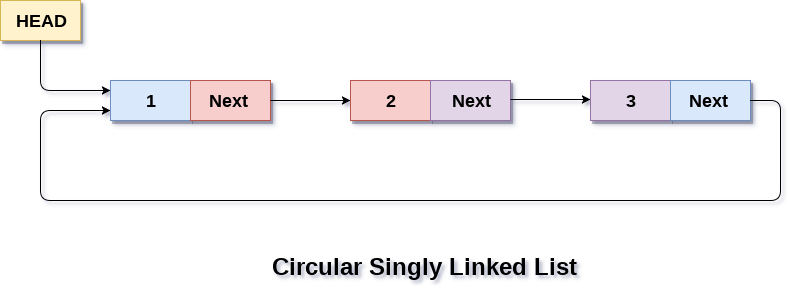
1. Circular Single Linked List

Di circular single linked list, node terakhir (tail) berisikan sebuah pointer yang terhubung ke node pertama (head), sehingga membentuk sebuah sirkuit, yang berarti tidak ada awal maupun akhir dan tidak ada NULL setelah node manapun, karena seperti contoh gambar dibawah, setelah node 3 adalah node 1.

Gambar berikut adalah contoh dari circular single linked list:

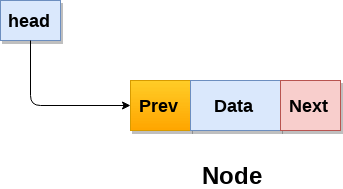
2. Doubly Linked List

Berbeda dengan circular single linked list, doubly linked list ini tidak membentuk sebuah sirkuit. Di setiap node ada sebuah pointer yang menunjuk ke node sebelum dan setelahnya. Dalam doubly linked list ini, setiap node berisikan 3 bagian: node data, pointer ke node berikutnya, dan pointer ke node sebelumnya.

Gambar berikut adalah contoh dari doubly linked list:

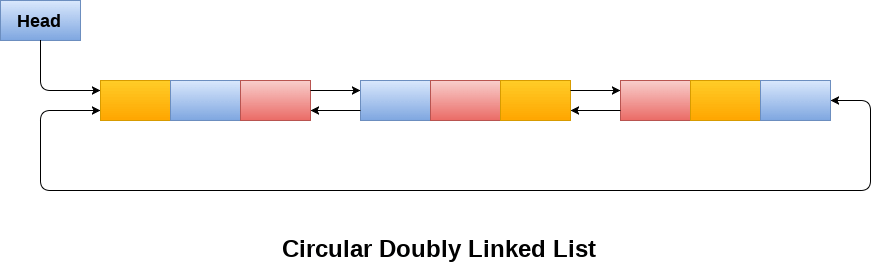
3. Circular Doubly Linked List

Sesuai dengan namanya, circular doubly linked list merupakan gabungan dari circular single linked list dan doubly linked list. circular doubly linked list tidak memiliki NULL di setiap nodenya karena seperti circular single linked list yang membentuk sebuah sirkuit. Tail berisikan alamat Head, dan juga sebaliknya.

Gambar berikut adalah contoh dari circular doubly linked list:

PUSH AND POP LINKED LIST

Dari materi yang diajarkan di kelas besar pada tanggal 3 Maret 2020, saya mempelajari cara menggunakan push dan pop dalam singly dan double linked list.

Push: Insert elemen ke dalam linked list

Pop: Kebalikannya push, menghilangkan elemen dari linked list

Contoh codingan pop pada singly linked list:

void pop()

{

curr = head;

while(curr->next!=tail){

curr = curr->next;

}

free(tail);

tail = curr;

tail->next = NULL;

}

Contoh codingan push pada double linked list:

void push(int a)

{

curr = (struct Data*)malloc(sizeof(struct Data);

curr->value = a;

if(head -- NULL){

head = tail = curr;

}

else

{

tail->next = curr;

curr->prev = tail;

tail = curr;

}

tail->next = NULL;

}

Contoh codingan pop pada double linked list:

void pop2()

{

if(tail == head){

free(curr);

tail = head = curr = NULL;

}

else

{

tail = tail->prev;

free(tail->next);

tail->next = NULL;

}

}

Dalam function pop, digunakan "free" untuk menghindari error dan crash saat dicompile.

Cara print semua value dalam linked list:

curr =head;

while(curr!=NULL){

printf("%d\n", curr->value);

curr = curr->next;

}

}

Baik single maupun double linked list, memiliki cara pop dan push yang hampir sama, namum perlu diperhatikan bahwa pada double linked list, current dapat berpindah ke node sebelumnya dengan prev.

Reminder:

Dalam single maupun double linked list, sebelum head dan setelah tail adalah NULL.

HASHING TABLE & BINARY TREE

Hashing adalah sebuah cara untuk mengetahui objek secara spesifik dari kumpulan objek yg mirip.

Sedangkan Hash Table adalah sebuah struktur data yang terdiri atas sebuah tabel dan fungsi yang bertujuan untuk memetakan nilai kunci yang unik untuk setiap record (baris) menjadi angka (hash) lokasi record tersebut dalam sebuah tabel.

Operasi pada hash table:

• insert: diberikan sebuah key dan nilai, insert nilai dalam tabel
• find: diberikan sebuah key, temukan nilai yang berhubungan dengan key
• remove: diberikan sebuah key,temukan nilai yang berhubungan dengan key, kemudian hapus nilai tersebut
• getIterator: mengambalikan iterator,yang memeriksa nilai satu demi satu

Contoh deklarasi hash table dalam coding:

HASHTBL *hashtbl_create(hash_size size, hash_size

(*hashfunc)(const char *))

{

HASHTBL *hashtbl;

if(!(hashtbl=malloc(sizeof(HASHTBL)))) return NULL;

free(hashtbl);

return NULL;

}

hashtbl->size=size;

if(hashfunc) hashtbl->hashfunc=hashfunc;

else hashtbl->hashfunc=def_hashfunc;

return hashtbl;

}

Binary Tree

Binary Tree merupakan bentuk struktur data yang tidak linier yang menggambarkan hubungan hierarchy (one to many) antara elemen-elemennya. Selain itu binary tree juga merupakan suatu tree dengan syarat bahwa tiap node hanya boleh memiliki maksimal 2 subtree dan kedua subtree tersebut tidak boleh saling berhubungan.

• Perfect binary tree, tiap nodenya (kecuali node terakhir) memiliki 2 child dan tiap subtree mempunyai panjang path yang sama

• Complete binary tree, subtree boleh memiliki panjang berbeda, selain node terakhir memili 0 atau 2 child

• Skewed binary tree, semua node kecuali node terakhir hanya memiliki 1 child

Hashing Table Implementation in Blockchain

Secara sederhana, hashing berarti mengambil string input dengan panjang berapa pun dan memberikan output dengan panjang tetap. Dalam konteks cryptocurrency seperti Bitcoin, transaksi diambil sebagai input dan dijalankan melalui algoritma hashing ( Bitcoin menggunakan SHA-256 ) yang memberikan output dengan panjang tetap.

BINARY SEARCH TREE

Binary Search Tree merupakan suatu struktur data binary tree yang menggunakan node sebagai dasarnya seperti halnya dengan linked list. Namun, BST ini digunakan untuk Fast Searching, Rapid Sorting, Easy Insertion, dan Deletion Data. Pada dasarnya, subtree sebelah kiri akan memiliki node yang nilainya lebih kecil daripada parent node, sedangkan sebelah kanan berisikan node yang memiliki nilai lebih tinggi daripada parent node.

Searching

Dalam mencari suatu nilai pada BST, pertama akan dibandingkan dengan nilai root, jika nilai yang dicari berada pada root, maka root adalah nilai yang dicari, namun jika nilai yang dicari lebih besar daripada root, maka akan mencari subtree sebelah kanan dari root node. Sebaliknya jika nilai yang dicari lebih kecil maka akan mencari subtree sebelah kiri dari root node.

Insertion

Memasukkan sebuah nilai baru pada binary tree akan selalu masuk ke bagian paling bawah (leaf). Dimulai dengan mencari nilai root sampai ke leaf node, dan jika nilai yang dimasukkan lebih kecil dari leaf node, maka angka yang dimasukkan akan berada di sebelah kiri leaf node, berlaku sebaliknya dengan nilai yang lebih besar.

Deletion

Ada beberapa kondisi dalam melakukan penghapusan dalam BST:

• Node yang akan dihapus adalah leaf node, dengan kata lain kita bisa langsung menghapus leaf node tersebut
• Node yang akan dihapus hanya memiliki 1 subtree, child node ini dicopy ke node yang akan dihapus, baru dilakukan penghapusan
• Node yang akan dihapus memilki 2 subtree, dapat dilakukan dengan 2 cara, yaitu dengan mengambil nilai maksimum dari sebelah kiri, atau dengan nilai minimum dari sebelah kanan.

SUMMARY & CODINGAN

Linked List II

1. Circular Single Linked List

Di circular single linked list, node terakhir (tail) berisikan sebuah pointer yang terhubung ke node pertama (head), sehingga membentuk sebuah sirkuit, yang berarti tidak ada awal maupun akhir dan tidak ada NULL setelah node manapun, karena seperti contoh gambar dibawah, setelah node 3 adalah node 1.

2. Doubly Linked List

Berbeda dengan circular single linked list, doubly linked list ini tidak membentuk sebuah sirkuit. Di setiap node ada sebuah pointer yang menunjuk ke node sebelum dan setelahnya. Dalam doubly linked list ini, setiap node berisikan 3 bagian: node data, pointer ke node berikutnya, dan pointer ke node sebelumnya.

3. Circular Doubly Linked List

Sesuai dengan namanya, circular doubly linked list merupakan gabungan dari circular single linked list dan doubly linked list. circular doubly linked list tidak memiliki NULL di setiap nodenya karena seperti circular single linked list yang membentuk sebuah sirkuit. Tail berisikan alamat Head, dan juga sebaliknya.

Push and Pop Linked List

Push: Insert elemen ke dalam linked list

Pop: Kebalikannya push, menghilangkan elemen dari linked list

Contoh codingan pop pada singly linked list:

void pop()

{

curr = head;

while(curr->next!=tail){

curr = curr->next;

}

free(tail);

tail = curr;

tail->next = NULL;

}

Contoh codingan push pada double linked list:

void push(int a)

{

curr = (struct Data*)malloc(sizeof(struct Data);

curr->value = a;

if(head -- NULL){

head = tail = curr;

}

else

{

tail->next = curr;

curr->prev = tail;

tail = curr;

}

tail->next = NULL;

}

Contoh codingan pop pada double linked list:

void pop2()

{

if(tail == head){

free(curr);

tail = head = curr = NULL;

}

else

{

tail = tail->prev;

free(tail->next);

tail->next = NULL;

}

}

Dalam function pop, digunakan "free" untuk menghindari error dan crash saat dicompile.

Cara print semua value dalam linked list:

curr =head;

while(curr!=NULL){

printf("%d\n", curr->value);

curr = curr->next;

}

}

Baik single maupun double linked list, memiliki cara pop dan push yang hampir sama, namum perlu diperhatikan bahwa pada double linked list, current dapat berpindah ke node sebelumnya dengan prev.

Hashing table & Binary Tree

Hashing Table

Hashing adalah sebuah cara untuk mengetahui objek secara spesifik dari kumpulan objek yg mirip.

Sedangkan Hash Table adalah sebuah struktur data yang terdiri atas sebuah tabel dan fungsi yang bertujuan untuk memetakan nilai kunci yang unik untuk setiap record (baris) menjadi angka (hash) lokasi record tersebut dalam sebuah tabel.

Operasi pada hash table:

insert: diberikan sebuah key dan nilai, insert nilai dalam tabel

find: diberikan sebuah key, temukan nilai yang berhubungan dengan key

remove: diberikan sebuah key,temukan nilai yang berhubungan dengan key, kemudian hapus nilai tersebut

getIterator: mengambalikan iterator,yang memeriksa nilai satu demi satu

Contoh deklarasi hash table dalam coding:

HASHTBL *hashtbl_create(hash_size size, hash_size

(*hashfunc)(const char *))

{

HASHTBL *hashtbl;

if(!(hashtbl=malloc(sizeof(HASHTBL)))) return NULL;

free(hashtbl);

return NULL;

}

hashtbl->size=size;

if(hashfunc) hashtbl->hashfunc=hashfunc;

else hashtbl->hashfunc=def_hashfunc;

return hashtbl;

}

Binary Tree

Binary Tree merupakan bentuk struktur data yang tidak linier yang menggambarkan hubungan hierarchy (one to many) antara elemen-elemennya. Selain itu binary tree juga merupakan suatu tree dengan syarat bahwa tiap node hanya boleh memiliki maksimal 2 subtree dan kedua subtree tersebut tidak boleh saling berhubungan.

• Perfect binary tree, tiap nodenya (kecuali node terakhir) memiliki 2 child dan tiap subtree mempunyai panjang path yang sama
• Complete binary tree, subtree boleh memiliki panjang berbeda, selain node terakhir memili 0 atau 2 child
• Skewed binary tree, semua node kecuali node terakhir hanya memiliki 1 child

Binary Search Tree

Binary Search Tree merupakan suatu struktur data binary tree yang menggunakan node sebagai dasarnya seperti halnya dengan linked list. Namun, BST ini digunakan untuk Fast Searching, Rapid Sorting, Easy Insertion, dan Deletion Data. Pada dasarnya, subtree sebelah kiri akan memiliki node yang nilainya lebih kecil daripada parent node, sedangkan sebelah kanan berisikan node yang memiliki nilai lebih tinggi daripada parent node.

Searching

Dalam mencari suatu nilai pada BST, pertama akan dibandingkan dengan nilai root, jika nilai yang dicari berada pada root, maka root adalah nilai yang dicari, namun jika nilai yang dicari lebih besar daripada root, maka akan mencari subtree sebelah kanan dari root node. Sebaliknya jika nilai yang dicari lebih kecil maka akan mencari subtree sebelah kiri dari root node.

Insertion

Memasukkan sebuah nilai baru pada binary tree akan selalu masuk ke bagian paling bawah (leaf). Dimulai dengan mencari nilai root sampai ke leaf node, dan jika nilai yang dimasukkan lebih kecil dari leaf node, maka angka yang dimasukkan akan berada di sebelah kiri leaf node, berlaku sebaliknya dengan nilai yang lebih besar.

Deletion

Ada beberapa kondisi dalam melakukan penghapusan dalam BST:

• Node yang akan dihapus adalah leaf node, dengan kata lain kita bisa langsung menghapus leaf node tersebut
• Node yang akan dihapus hanya memiliki 1 subtree, child node ini dicopy ke node yang akan dihapus, baru dilakukan penghapusan
• Node yang akan dihapus memilki 2 subtree, dapat dilakukan dengan 2 cara, yaitu dengan mengambil nilai maksimum dari sebelah kiri, atau dengan nilai minimum dari sebelah kanan.

CODINGAN

Saya telah meletakkan hasil codingan saya berdasarkan soal yang diberikan pada link berikut:

https://drive.google.com/file/d/1xdUejwUVLh9oxKrTu37yf9cA0AdPClHL/view?usp=sharing

AVL TREE

AVL tree adalah sebuah Binary Search Tree yang bisa menyeimbangkan antara tinggibagian kiri dengan tinggi bagian kanan.

Contoh sebuah AVL Tree

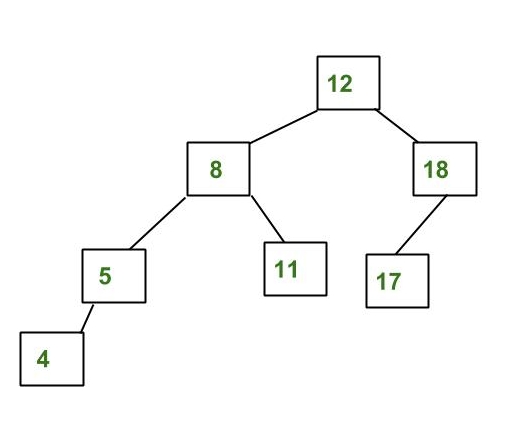
Perbedaan tinggi subtree bagian kanan dan kiri adalah kurang dari sama dengan 1.

Contoh yang bukan AVL Tree

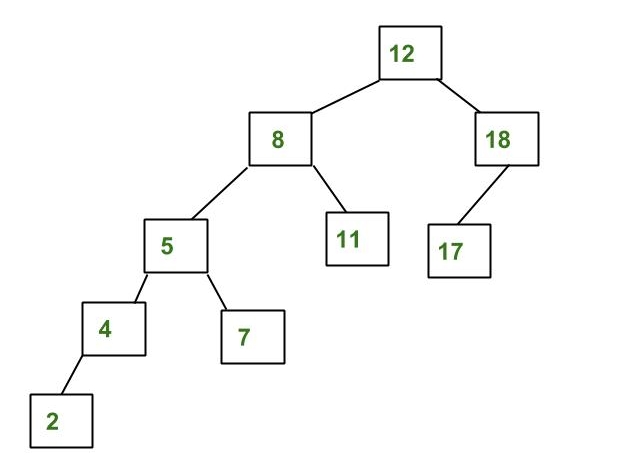
Perbedaan tinggi subtree 8 dan 18 lebih dari 1.

AVL Tree sangat berguna karena BST biasa yang bukan AVL Tree, membutuhkan waktu yang cukup lama untuk beroperasi.

Insertion

Proses insertion AVL Tree dan BST cukup mirip, hanya saja setelah diinsert, AVL Tree langsung menyeimbangkan subtree kiri dan kanan.

Contoh X adalah node yang akan diinsert,

• Case 1 : node terdalam terletak pada subtree kiri dari anak kiri X (left-left)
• Case 2 : node terdalam terletak pada subtree kanan dari anak kanan X (right-right)
• Case 3 : node terdalam terletak pada subtree kanan dari anak kiri X (right-left)
• Case 4 : node terdalam terletak pada subtree kiri dari anak kanan X (left-right

Case tersebut akan selesai menggunakan single rotation untuk case 1 dan 2, gunakan double rotation untuk case 3 dan 4.

Contoh left rotation

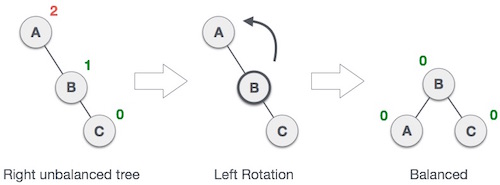
HEAP AND TRIES

Heap

Heap adalah pohon complete binary tree biner yang berdasarkan memenuhi properti heap. Property heaps antara lain :

Min Heap

Setiap node lebih kecil dari masing-masing childnya

Root merupakan node paling kecil, sedangkan node terbesar terletak pada leaf node

           10                     10

         /    \                /      \ 

       20      100            15        30 

      /                      /  \      /  \

    30                     40    50  100   40

Max Heap

Setiap node lebih besar dari masing-masing childnya

Root merupakan node paling besar, sedangkan node terkecil terletak pada leaf node

Min-Max Heap

Heap dengan Min heap pada level ganjil dan Max heap pada level genap

Heap dapat diimplementasi dengan array maupun dengan linked list. Aplikasi heap adalah sebagai berikut:

Priority Queue

1. Selection algorithm
2. Dijkstra's Algorithm
3. Prim Algorithm

Implementasi heap menggunakan array :

• Array dimulai dengan indeks ke 1
• Rumus umum aplikasi heap dengan array (x adalah current node):
• Parent(x): x/2
• Left-child(x): 2*x
• Right-Child(x): 2*x+1

Tries

Tries atau prefix tree adalah sebuah tree yang tersusun/berurutan pada struktur data yang digunakan untuk menyimpan kumpulan array (biasanya berupa string). 

TRIES berasal dari kata RETRIEVAL, karena tries dapan menemukan sebuat kata dalam kamis dengan hanya dengan menggunakan kata depan dari kata tersebut.

Pengaplikasian Tries

Tries digunakan untuk search dalam sebuah web browser untuk menunjukkan auto-complete saat mencari, contohnya setelah mengetik "goo", system akan menunjukkan beberapa pilihan yang mungkin ingin kita cari seperti "google".